Cette partie est la troisième d’une série de quatre pour le développement d’un jeu de type plateforme. Assurez-vous d’avoir parcouru les sections précédentes.
Dans la seconde partie, nous avons vu comment animer Bob, cependant les mouvement étaient un peu saccadé. Dans cet article, nous allons faire sauter Bob et améliorer son mouvement de façon à le rendre plus naturel. Nous allons donc devoir faire un rappel sur les notions de physique du secondaire (ou lycée). De plus, nous allons nettoyer un peu le code des articles précédents.
La physique du saut
Sauter est l’action d’une entité (Bob) qui applique une force qui lui permet de se propulser dans les airs et de retomber au sol (substrat). Cette action peut être achevé en appliquant une force supérieure à celle qui est exercé au niveau du sol (gravité).
En identifiant les différents éléments, nous avons :
- Bob – Entité
- Sol – Substrat
- Gravité (g) – Force constante qui s’applique sur toutes les entités du monde.
Pour implanter un saut réaliste, nous allons simplement appliquer les
lois du mouvement de Newton. Si nous ajoutons les propriétés nécessaires (masse, gravité et friction) à Bob et au monde, alors nous avons tous les éléments nécessaires pour implanter le saut.
Prenez note de la prochaine illustration et de ses composantes. La partie de gauche est lorsque nous maintenons la touche « saut » et la partie de droite montre Bob pendant un saut.
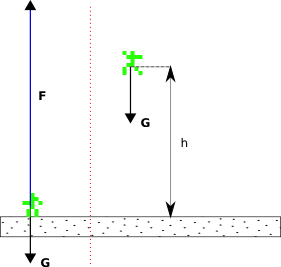
Examinons les forces dans différents états de Bob.
Bob est
inactif et sur le sol
(la terre).
Dans ce cas, seule la
gravité agit sur Bob. Cela signifie que Bob est tiré vers le bas avec une force constante.
La formule permettant de calculer la force qui tire un objet à la masse est

où
m est la
masse (poids bien penser n’est pas poids) et
a est
l’accélération.
Simplifions les choses et considérons Bob comme ayant une masse de
1 si la force est égale à l’accélération.
Si l’on applique une force constante à un objet, sa
vitesse augmente infiniment.
La formule pour calculer la vitesse d’un objet est:

où
- v – est la vitesse finale
- u – est la vitesse initiale
- a – est l’accélération
- t – est le temps écoulé depuis que l’accélération est appliquée
Si nous plaçons Bob au milieu des airs cela nous indique que la vitesse initiale est 0. Si nous considérons que l’accélération gravitationnelle de la Terre est de 9,8 et le poids de Bob (masse) est 1, alors il est facile de calculer sa vitesse de chute après une seconde.

Ainsi, après une seconde en chute libre, Bob a accéléré de 0 à 9,8 mètres par seconde, ce qui représente 35,28 km/h. C’est très rapide.
Si nous voulons connaître sa vitesse après une deuxième seconde nous devrions utiliser la même formule.

C’est 70,56 km/h ce qui est très rapide comme variation.
On voit déjà que l’accélération est linéaire et que, sous une force constante un objet va accélérer l’infini. Ceci est dans un environnement idéal où il n’y a pas de frottement et de traînée. Parce que l’air offre de la friction et elle s’applique aussi aux forces qui sont impliquées dans la chute d’un objet. En tombant, l’objet atteindra éventuellement une
vitesse terminale, ainsi l’accélération n’aura plus aucun effet. Cela dépend de beaucoup de facteurs que nous allons ignorer pour nos besoins.
Une fois l’objet en chute a touché le sol, il s’arrête, la gravité ne l’affectera pas plus. Ce n’est pas vrai cependant, la gravité s’applique toujours, cependant nous ne construisons pas un simulateur complet de physique, mais un jeu où Bob ne sera pas tué s’il touche le sol à la vitesse terminale.
En reformulant le dernier paragraphe, nous vérifions si Bob a touché le sol, et si c’est le cas, alors nous allons ignorer la gravité.
Faisons sauter Bob!
Pour faire Bob sauté, nous avons besoin d’une force dirigée opposé à la gravité (vers le haut) qui annule non seulement l’effet de la gravité, mais propulse Bob dans l’air. Si vous vérifiez la figure précédente, la force (
f) est beaucoup plus forte (son
amplitude ou sa
durée est beaucoup plus grande que celle du vecteur de la gravité). En ajoutant les 2 vecteurs ensemble (G et F), on obtient la force finale qui va agir sur Bob.
Pour simplifier les choses, nous allons nous débarrasser de vecteurs et ne travailler qu’avec leurs composantes Y.
Sur Terre,

. Vu que la gravité « pointe » vers le bas, nous allons utiliser la forme négative

. Quand Bob saute, il ne fait rien de plus que de générer suffisamment de force pour produire assez d’accélération qui va l’amener à la hauteur (
h) avant que la gravité (
g) ne le ramène au sol.
Parce que Bob est un être humain comme nous, il ne peut pas maintenir l’accélération une fois qu’il est dans les airs, du moins sans un jetpack. Pour simuler ceci, nous pourrions créer une force énorme lorsque l’on appuie sur la touche «saut». En appliquant les formules ci-dessus, la vitesse initiale sera suffisamment élevée pour faire en sorte que même la gravité agissant sur Bob ne sera pas assez forte pour l’empêcher de grimper vers une certaine hauteur. Après un certain temps, il commencera sa chute libre.
Si nous appliquons cette méthode, nous aurons un beau saut réaliste.
Si nous vérifions soigneusement le jeu de Star Guard, le héros peut sauter à des hauteurs différentes selon le temps d’appuie sur le bouton de saut. Ceci est facilement implémentable si nous gardons la force vers le haut appliquée aussi longtemps que nous nous maintenons la touche de saut enfoncée. Après un certain temps, nous coupons le bouton pour s’assurer que Bob ne démarre pas à voler.
L’implémentation du saut
Assez de physique pour l’instant! Voyons comment nous allons implémenter le saut.
Renommez WorldController.java pour BobController.java. Cela fait plus de sens, car nous contrôlons Bob.
public class BobController {
enum Keys {
LEFT, RIGHT, JUMP, FIRE
}
private static final long LONG_JUMP_PRESS = 150l;
private static final float ACCELERATION = 20f;
private static final float GRAVITY = -20f;
private static final float MAX_JUMP_SPEED = 7f;
private static final float DAMP = 0.90f;
private static final float MAX_VEL = 4f;
// temporaire pour l'exercice
private static final float WIDTH = 10f;
private World world;
private Bob bob;
private long jumpPressedTime;
private boolean jumpingPressed;
// ... code omis ... //
public void jumpReleased() {
keys.get(keys.put(Keys.JUMP, false));
jumpingPressed = false;
}
// ... code omis ... //
public void update(float delta) {
// Gestion des entrées
processInput();
// Régler la gravité à l'acceleration
bob.getAcceleration().y = GRAVITY;
// Conversion de l'accélération dans le bon temps.
bob.setAcceleration(new Vector2(bob.getAcceleration().x*delta,bob.getAcceleration().y*delta));
// Application de l'accélération pour avoir la bonne vitesse
bob.getVelocity().add(bob.getAcceleration().x, bob.getAcceleration().y);
// S'il n'y a plus d'accélération, on ralenti Bob en X pour la friction
if (bob.getAcceleration().x == 0)
bob.getVelocity().x *= DAMP;
// On limite la vitesse de déplacement en X de Bob
if (bob.getVelocity().x > MAX_VEL)
bob.getVelocity().x = MAX_VEL;
if (bob.getVelocity().x < -MAX_VEL)
bob.getVelocity().x = -MAX_VEL;
bob.update(delta);
if (bob.getPosition().y < 0) {
bob.getPosition().y = 0f;
bob.setPosition(bob.getPosition());
if (bob.getState().equals(State.JUMPING)) {
bob.setState(State.IDLE);
}
}
if (bob.getPosition().x < 0) {
bob.getPosition().x = 0;
bob.setPosition(bob.getPosition());
if (!bob.getState().equals(State.JUMPING)) {
bob.setState(State.IDLE);
}
}
if (bob.getPosition().x > WIDTH - bob.getBounds().width ) {
bob.getPosition().x = WIDTH - bob.getBounds().width;
bob.setPosition(bob.getPosition());
if (!bob.getState().equals(State.JUMPING)) {
bob.setState(State.IDLE);
}
}
}
private boolean processInput(){
if (keys.get(Keys.JUMP)){
// Bob saute!
if (!bob.getState().equals(State.JUMPING)){
jumpingPressed = true;
jumpPressedTime = System.currentTimeMillis();
bob.setState(State.JUMPING);
bob.getVelocity().y = MAX_JUMP_SPEED;
}
else
{
// On limite le temps que l'on maintient le bouton appuyé
if (jumpingPressed &&
((System.currentTimeMillis() - jumpPressedTime) >= LONG_JUMP_PRESS)){
jumpingPressed = false;
}
else
{
if (jumpingPressed){
bob.getVelocity().y = MAX_JUMP_SPEED;
}
}
}
}
if (keys.get(Keys.LEFT))
{
bob.setFacingLeft(true);
if (!bob.getState().equals(State.JUMPING)){
bob.setState(Bob.State.WALKING);
}
bob.getAcceleration().x = -ACCELERATION;
}
else if (keys.get(Keys.RIGHT))
{
bob.setFacingLeft(false);
if (!bob.getState().equals(State.JUMPING)){
bob.setState(Bob.State.WALKING);
}
bob.getAcceleration().x = ACCELERATION;
}
else
{
if (!bob.getState().equals(State.JUMPING)){
bob.setState(State.IDLE);
}
bob.getAcceleration().x = 0;
}
return false;
}
}
Voici l’analyse du code :
- Les constantes
- LONG_JUMP_PRESS est le temps en millisecondes que l’on permet l’application de la force du saut. Plus longtemps le bouton est maintenu, plus haut Bob sautera.
- ACCELERATION ceci permet la gestion de la course. C’est exactement le même principe que le saut.
- GRAVITY ceci est l’accélération gravitationnelle.
- MAX_JUMP_SPEED c’est la vitesse maximale du saut.
- DAMP est la friction appliquée à Bob lorsqu’il se déplace en X. Ainsi si l’on arrête d’accélérer, à chaque tour la vitesse de Bob diminuera de 10%.
- MAX_VEL idem que MAX_JUMP_SPEED mais sur l’axe des X.
- La variable temporaire servira à limiter le déplacement de Bob sur l’axe des X.
- jumpPressedTime est l’accumulateur de temps pour vérifier combien de temps que la touche saut a été maintenu.
- jumpPressed est un booléen indiquant si la touche du saut a été appuyée.
- processInput
- On vérifie si le saut a été activé
- Dans le cas où Bob ne saute pas, on modifie sont état à JUMPING, on indique que le bouton saut est appuyé, on accumule le temps que le bouton est maintenu et on applique la vitesse maximale à la vitesse de Bob.
- Si l’état de Bob était déjà à saut, on vérifie le temps que le bouton est maintenu. Si ce dernier est plus long que le temps maximum, on désactive le bouton. Sinon, on applique encore de la vitesse à la vitesse en Y de Bob.
Rafraîchissement de code
Dans les images fournies, nous avons deux images qui représentent Bob dans l’ascension du saut ainsi que la descente. Nous allons les rajouter à WorldRenderer.
- Étant donné que Bob n’entre pas encore en contact avec les blocs, nous allons commenter la ligne drawBlocks() dans la méthode render() de WorldRenderer.
- Ajoutons la méthode setDebug() dans WorldRenderer et permettons la lecture de la touche D pour permettre l’activation et désactivation du mode de débogage dans le GameScreen.
- Nous allons définir de nouvelle texture pour le saut de Bob soient bobJumpLeft et bobFallLeft ainsi qui leur opposé. Lorsque la vitesse en Y sera positive, on affichera Bob sautant et lorsqu’elle sera négative, ce sera celle lorsqu’il tombe.
public class WorldRenderer {
// ... omis ... //
private TextureRegion bobJumpLeft;
private TextureRegion bobFallLeft;
private TextureRegion bobJumpRight;
private TextureRegion bobFallRight;
private void loadTextures() {
TextureAtlas atlas = new TextureAtlas(Gdx.files.internal("images/textures/textures.atlas"));
// ... omis ... //
bobJumpLeft = atlas.findRegion("bob-up");
bobJumpRight = new TextureRegion(bobJumpLeft);
bobJumpRight.flip(true, false);
bobFallLeft = atlas.findRegion("bob-down");
bobFallRight = new TextureRegion(bobFallLeft);
bobFallRight.flip(true, false);
}
private void drawBob() {
Bob bob = world.getBob();
bobFrame = bob.isFacingLeft() ? bobIdleLeft : bobIdleRight;
if(bob.getState().equals(State.WALKING)) {
bobFrame = bob.isFacingLeft() ? walkLeftAnimation.getKeyFrame(bob.getStateTime(), true) : walkRightAnimation.getKeyFrame(bob.getStateTime(), true);
} else if (bob.getState().equals(State.JUMPING)) {
if (bob.getVelocity().y > 0) {
bobFrame = bob.isFacingLeft() ? bobJumpLeft : bobJumpRight;
} else {
bobFrame = bob.isFacingLeft() ? bobFallLeft : bobFallRight;
}
}
spriteBatch.draw(bobFrame, bob.getPosition().x * ppuX, bob.getPosition().y * ppuY, Bob.getSize() * ppuX, Bob.getSize() * ppuY);
}
}
Texte de fin
 Examinons les forces dans différents états de Bob.
Bob est inactif et sur le sol (la terre).
Dans ce cas, seule la gravité agit sur Bob. Cela signifie que Bob est tiré vers le bas avec une force constante.
La formule permettant de calculer la force qui tire un objet à la masse est
Examinons les forces dans différents états de Bob.
Bob est inactif et sur le sol (la terre).
Dans ce cas, seule la gravité agit sur Bob. Cela signifie que Bob est tiré vers le bas avec une force constante.
La formule permettant de calculer la force qui tire un objet à la masse est
 où m est la masse (poids bien penser n’est pas poids) et a est l’accélération.
Simplifions les choses et considérons Bob comme ayant une masse de 1 si la force est égale à l’accélération.
Si l’on applique une force constante à un objet, sa vitesse augmente infiniment.
La formule pour calculer la vitesse d’un objet est:
où m est la masse (poids bien penser n’est pas poids) et a est l’accélération.
Simplifions les choses et considérons Bob comme ayant une masse de 1 si la force est égale à l’accélération.
Si l’on applique une force constante à un objet, sa vitesse augmente infiniment.
La formule pour calculer la vitesse d’un objet est:
 où
où
 Ainsi, après une seconde en chute libre, Bob a accéléré de 0 à 9,8 mètres par seconde, ce qui représente 35,28 km/h. C’est très rapide.
Si nous voulons connaître sa vitesse après une deuxième seconde nous devrions utiliser la même formule.
Ainsi, après une seconde en chute libre, Bob a accéléré de 0 à 9,8 mètres par seconde, ce qui représente 35,28 km/h. C’est très rapide.
Si nous voulons connaître sa vitesse après une deuxième seconde nous devrions utiliser la même formule.
 C’est 70,56 km/h ce qui est très rapide comme variation.
On voit déjà que l’accélération est linéaire et que, sous une force constante un objet va accélérer l’infini. Ceci est dans un environnement idéal où il n’y a pas de frottement et de traînée. Parce que l’air offre de la friction et elle s’applique aussi aux forces qui sont impliquées dans la chute d’un objet. En tombant, l’objet atteindra éventuellement une vitesse terminale, ainsi l’accélération n’aura plus aucun effet. Cela dépend de beaucoup de facteurs que nous allons ignorer pour nos besoins.
Une fois l’objet en chute a touché le sol, il s’arrête, la gravité ne l’affectera pas plus. Ce n’est pas vrai cependant, la gravité s’applique toujours, cependant nous ne construisons pas un simulateur complet de physique, mais un jeu où Bob ne sera pas tué s’il touche le sol à la vitesse terminale.
En reformulant le dernier paragraphe, nous vérifions si Bob a touché le sol, et si c’est le cas, alors nous allons ignorer la gravité.
C’est 70,56 km/h ce qui est très rapide comme variation.
On voit déjà que l’accélération est linéaire et que, sous une force constante un objet va accélérer l’infini. Ceci est dans un environnement idéal où il n’y a pas de frottement et de traînée. Parce que l’air offre de la friction et elle s’applique aussi aux forces qui sont impliquées dans la chute d’un objet. En tombant, l’objet atteindra éventuellement une vitesse terminale, ainsi l’accélération n’aura plus aucun effet. Cela dépend de beaucoup de facteurs que nous allons ignorer pour nos besoins.
Une fois l’objet en chute a touché le sol, il s’arrête, la gravité ne l’affectera pas plus. Ce n’est pas vrai cependant, la gravité s’applique toujours, cependant nous ne construisons pas un simulateur complet de physique, mais un jeu où Bob ne sera pas tué s’il touche le sol à la vitesse terminale.
En reformulant le dernier paragraphe, nous vérifions si Bob a touché le sol, et si c’est le cas, alors nous allons ignorer la gravité.
 . Vu que la gravité « pointe » vers le bas, nous allons utiliser la forme négative
. Vu que la gravité « pointe » vers le bas, nous allons utiliser la forme négative  . Quand Bob saute, il ne fait rien de plus que de générer suffisamment de force pour produire assez d’accélération qui va l’amener à la hauteur (h) avant que la gravité (g) ne le ramène au sol.
Parce que Bob est un être humain comme nous, il ne peut pas maintenir l’accélération une fois qu’il est dans les airs, du moins sans un jetpack. Pour simuler ceci, nous pourrions créer une force énorme lorsque l’on appuie sur la touche «saut». En appliquant les formules ci-dessus, la vitesse initiale sera suffisamment élevée pour faire en sorte que même la gravité agissant sur Bob ne sera pas assez forte pour l’empêcher de grimper vers une certaine hauteur. Après un certain temps, il commencera sa chute libre.
Si nous appliquons cette méthode, nous aurons un beau saut réaliste.
Si nous vérifions soigneusement le jeu de Star Guard, le héros peut sauter à des hauteurs différentes selon le temps d’appuie sur le bouton de saut. Ceci est facilement implémentable si nous gardons la force vers le haut appliquée aussi longtemps que nous nous maintenons la touche de saut enfoncée. Après un certain temps, nous coupons le bouton pour s’assurer que Bob ne démarre pas à voler.
. Quand Bob saute, il ne fait rien de plus que de générer suffisamment de force pour produire assez d’accélération qui va l’amener à la hauteur (h) avant que la gravité (g) ne le ramène au sol.
Parce que Bob est un être humain comme nous, il ne peut pas maintenir l’accélération une fois qu’il est dans les airs, du moins sans un jetpack. Pour simuler ceci, nous pourrions créer une force énorme lorsque l’on appuie sur la touche «saut». En appliquant les formules ci-dessus, la vitesse initiale sera suffisamment élevée pour faire en sorte que même la gravité agissant sur Bob ne sera pas assez forte pour l’empêcher de grimper vers une certaine hauteur. Après un certain temps, il commencera sa chute libre.
Si nous appliquons cette méthode, nous aurons un beau saut réaliste.
Si nous vérifions soigneusement le jeu de Star Guard, le héros peut sauter à des hauteurs différentes selon le temps d’appuie sur le bouton de saut. Ceci est facilement implémentable si nous gardons la force vers le haut appliquée aussi longtemps que nous nous maintenons la touche de saut enfoncée. Après un certain temps, nous coupons le bouton pour s’assurer que Bob ne démarre pas à voler.
Laisser un commentaire