Nombre aléatoire
Un nombre aléatoire est un nombre que l’on ne peut généralement prédire. En programmation, un nombre généré aléatoirement est un nombre réel compris entre 0 et 1. Les nombres générés sont distribués de manière uniforme, c’est-à-dire que les probabilités sont égales pour tous les nombres comme un dé.
On utilise les nombres aléatoires dans plusieurs domaines d’application tel que les jeux vidéo, la génération de données, l’intelligence artificielle, etc.
On remarque que la distribution est uniforme. C’est comme un dé que l’on lance. On a autant de probabilité d’obtenir un 2 qu’un 6.
La fonction que l’on retrouvera dans Processing sera
random() qui retourne une valeur entre 0 et 1.
Distribution normale
Une distribution normale suit ce qu’on appelle une distribution gaussienne.
Disons que l’on désire générer une population de zombies. Chaque zombie a une taille donnée en mètre. Dans une population réelle, la taille des zombies ne suit pas une distribution uniforme, c’est-à-dire qu’il y a plus de chance que l’on tombe sur un zombie de 1.72 mètre qu’un zombie de 2 mètres. Dans ma population, j’ai plus de zombies qui ont des tailles variants entre 1.65 et 1.75 mètre que des individus de 2 mètres et plus. La même chose pour des zombies de moins de 1.50 mètres.
La hauteur des populations animales suit généralement une distribution normale. Ainsi, il y a une concentration des hauteurs plus fréquentes autour de la moyenne qu’aux extrêmes.
Dans l’exemple qui suit, nous avons une distribution normale avec une moyenne de 24 et un écart-type de 5.
La fonction que l’on retrouvera dans Processing sera
randomGaussian() qui retourne une valeur avec une moyenne de 0 et un écart-type de 1.
Exemple de cas d’utilisation
Disons que l’on désire réaliser un jeu de biathlon (ski de fond et tir) dans lequel le joueur a une carabine. Lorsque le joueur effectue du ski à pleine puissance pendant une certaine période il s’épuise et s’il skie tranquillement longtemps son énergie revient. Lorsque le joueur vise avec son télescope, la mire bouge au gré de la fatigue du personnage. Pour rendre le jeu réaliste, le déplacement de la mire sera plus grand lorsque le personnage sera fatigué. Ainsi on augmentera l’écart-type en X et en Y pour évaser la courbe de distribution.
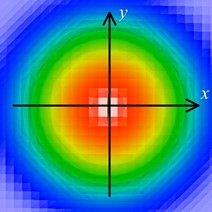 |
Dans l’exemple ci-contre, la zone rouge est chaude et bleue froide. Ainsi, la dimension de la zone rouge est inversement proportionnelle à l’écart-type en X et Y |
Distribution normale, courbe gaussienne et courbe en cloche sont tous des synonymes.
Exercice
Faire ces petits exercices à l’aide de Processing ou p5.js. PS : Doit être en POO.
- Animer un point qui doit se déplacer de manière aléatoire
- Modifier le projet pour que le point tende vers la gauche dans 40% des cas.
- Lorsque l’utilisateur clique avec la souris, faire apparaître des cercles de manière aléatoire à proximité du pointeur, mais tout en gardant une distribution normale avec une moyenne de 0 et un écart-type de 10 sur les deux axes.




Laisser un commentaire